Найти функцию распределения F(x). Непрерывные случайные величины Случайная величина х задана функцией
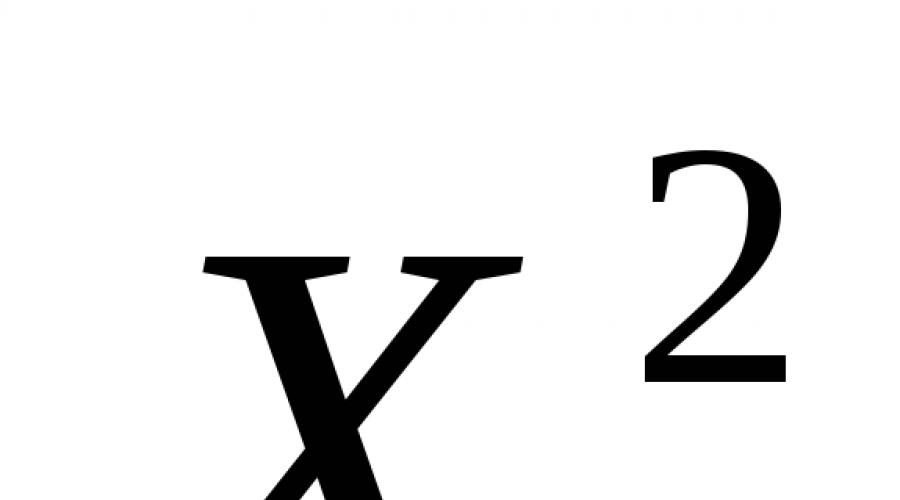
Проверим,
выполняется ли требование равномерной
ограниченности дисперсии. Напишем
закон распределения
:
|
|
|
|
|
|
|
Найдём
математическое ожидание
:
Найдём
дисперсию
:
Эта функция возрастает, следовательно, чтобы вычислить константу, ограничивающую дисперсию, можно вычислить предел:
Таким образом, дисперсии заданных случайных величин неограниченны, что и требовалось доказать.
Б) Из формулировки теоремы Чебышева следует, что требование равномерной ограниченности дисперсий является достаточным, но не необходимым условием, поэтому нельзя утверждать, что к данной последовательности эту теорему применить нельзя.
Последовательность независимых случайных величин Х 1 , Х 2 , …, Х n , … задана законом распределения
D(X n)=M(X n 2)- 2 ,
учитывай, что M(X n)=0, найдем (выкладки предоставляются выполнить читателю)
Временно предположим, что n изменяется непрерывно (чтобы подчеркнуть это допущение, обозначим n через х), и исследуем на экстремум функцию φ(х)=х 2 /2 х-1 .
Приравняв первую производную этой функции к нулю, найдем критические точки х 1 =0 и х 2 =ln 2.
Отбросим первую точку как не представляющую интереса (n не принимает значения, равного нулю); легко видеть, что в точек х 2 =2/ln 2 функция φ(х) имеет максимум. Учитывая, что 2/ln 2 ≈ 2.9 и что N – целое положительное число, вычислим дисперсию D(X n)= (n 2 /2 n -1)α 2 для ближайших к числу 2.9 (слева и справа) целых чисел, т.е. для n=2 и n=3.
При n=2 дисперсия D(X 2)=2α 2 , при n=3 дисперсия D(Х 3)=9/4α 2 . Очевидно,
(9/4)α 2 > 2α 2 .
Таким образом, наибольшая возможная дисперсия равна (9/4)α 2 , т.е. дисперсии случайных величин Хn равномерно ограничены числом (9/4)α 2 .
Последовательность независимых случайных величин X 1 , X 2 , …, X n , … задана законом распределения
Применима ли к заданной последовательности теорема Чебышева?
Замечание. Поскольку случайные величины Х, одинаково распределены и независимы, то читатель, знакомый с теоремой Хинчина, может ограничиться вычислением лишь математического ожидания и убедиться, что оно кончено.
Поскольку случайные величины Х n независимы, то они подавно и попарно независимы, т.е. первое требование теоремы Чебышева выполняется.
Легко найти, что M(X n)=0, т.е.первое требование конечности математических ожиданий выполняется.
Остается проверить выполнимость требования равномерной ограниченности дисперсий. По формуле
D(X n)=M(X n 2)- 2 ,
учитывай, что M(X n)=0, найдем
Таким образом, наибольшая возможная дисперсия равна 2, т.е. дисперсии случайных величин Х n равномерно ограничены числом 2.
Итак, все требования теоремы Чебышева выполняются, следовательно, к рассматриваемой последовательности эта теорема применима.
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1/3).
Случайная
величина Х задана на всей оси Ох функцией
распределена F(x)=1/2+(arctg
x)/π. Найти
вероятность того, что в результате
испытания величина Х примет значение,
заключенное в интервале (0, 1). Вероятность
того, что Х примет значение, заключенное
в интервале (a, b),
равна приращению функции распределения
на этом интервале: P(a Р(0<
Х <1) = F(1)-F(0)
= x =1 -
x =0
= 1/4 Случайная
величина Х функцией распределения Найти
вероятность того, что в результате
испытания величина Х примет значение,
заключенное в интервале (-1, 1). Вероятность
того, что Х примет значение, заключенное
в интервале (a, b),
равна приращению функции распределения
на этом интервале: P(a Р(-1<
Х <1) = F(1)-F(-1)
= x =-1
– x =1
= 1/3. Функция
распределения непрерывной случайной
величины Х (времени безотказной работы
некоторого устройства) равна
F(х)=1-е -х/ T (х≥0).
Найти вероятность безотказной работы
устройства за время х≥Т. Вероятность
того, что Х примет значение, заключенное
в интервале x≥T,
равна приращению функции распределения
на этом интервале: P(0 P(x≥T)
= 1 - P(T Случайная
величина Х задана функцией распределения Найти
вероятность того, что в результате
испытания Х примет значение: а) меньшее
0.2; б) меньшее трех; в) не меньшее трех;
г) не меньшее пяти. а)
Так как при х≤2 функция F(х)=0,
то F(0, 2)=0, т.е. P(х
< 0, 2)=0; б)
Р(Х < 3) = F(3) = x =3
= 1.5-1 = 0.5; в)
события Х≥3 и Х<3 противоположны,
поэтому Р(Х≥3)+Р(Х<3)=1. Отсюда, учитывая,
что Р(Х<3)=0.5 [см. п. б.], получим Р(Х≥3) =
1-0.5 = 0.5; г)
сумма вероятностей противоположных
событий равна единице, поэтому
Р(Х≥5)+Р(Х<5)=1. Отсюда, используя условие,
в силу которого при х>4 функция F(x)=1,
получим Р(Х≥5) = 1-Р(Х<5) = 1-F(5)
= 1-1 = 0. Случайная
величина Х задана функцией распределния Найти
вероятность того, что в результате
четырех независимых испытаний величина
Х ровно три раза примет значение,
принадлежащее интервалу (0.25, 0.75). Вероятность
того, что Х примет значение, заключенное
в интервале (a, b),
равна приращению функции распределения
на этом интервале: P(a P(0.25< X <0.75) =
F(0.75)-F(0.25) =
0.5 Следовательно,
,
или
Случайная
величина X задана на всей
оси Ox функцией распределения
.
Найти возможное значения
,
удовлетворяющее условию: с вероятностью
случайная
X в результате испытания
примет значение большее
Решение.
События
и
- противоложные, поэтому
.
Следовательно,
.
Так как
,
то
. По
определению функции распределения,
. Следовательно,
,
или
Дискретная
случайная величина X задана
законом распределения Итак,
искомая функция распределения имеет
вид Дискретная
случайная величина X
задана законом распределения Найти
функцию распределения
и
начертить ее график. Дана
функция распределения непрерывной
случайной величины X Найти
плотность распределения f(x). Плотность
распределения равна первой производной
от функции распределения: Непрерывная
случайная величина X
задана плотностью распределения
в
интервале
;
вне этого интервала
.
Найти вероятность того, что X
примет значение, принадлежащее интервалу
. Воспользуемся
формулой
.
По условию
,и
.
Следовательно, искомая вероятность Непрерывная
случайная величина X
задана плотностью распределения
Воспользуемся
формулой
.
По условию
,и
Плотность
распределения непрерывной случайной
величины Х в интервале (-π/2,
π/2) равна f(x)=(2/π)*cos2x
; вне этого интервала f(x)=0.
Найти вероятность того, что в трех
независимых испытаниях Х примет ровно
два раза значение, заключенное в интервале
(0, π/4). Воспользуемся
формулой Р(a Р(0 Ответ:
π+24π. fx=0,
при x≤0cosx,
при 0 Используем
формулу Если
х ≤0, то f(x)=0,
следовательно, F(x)=-∞00dx=0. Если
0 F(x)=-∞00dx+0xcosxdx=sinx. Если
x≥ π2 , то F(x)=-∞00dx+0π2cosxdx+π2x0dx=sinx|0π2=1. Итак,
искомая функция распределения Fx=0,
при x≤0sinx,
при 0 Задана
плотность распределения непрерывной
случайной величины Х: Fx=0,
при x≤0sinx,
при 0 Найти
функцию распределения F(x). Используем
формулу Плотность
распределения непрерывной случайной
величины Х задана на всей оси Ох равеством
.
Найти постоянный параметр С. Таким образом, Плотность
распределения непрерывной случайной
величины
задана
на всей оси
равенством
Найти
постоянный параметр С. Решение.
Плотность распределения
должна удовлетворять условию
.
Потребуем, чтобы это условие выполнялось
для заданной функции: Найдем
сначала неопределенный интеграл: Затем вычислим несобственный интеграл: Таким образом, Подставив
(**) в (*), окончательно получим
. Плотность
распределения непрерывной
случайной величины X в
интервале
равна
;
вне этого интервала f(х) = 0. Найти постоянный
параметр С. Найдем
сначала неопределенный интеграл: Затем вычислим несобственный интеграл: Подставив
(**) в (*), окончательно получим
. Плотность
распределения непрерывной случайной
величины Х задана в интервале
равенством
;
вне этого интервала f(х) = 0. Найти
постоянный параметр С. Решение.
Плотность распределения
должна удовлетворять условию
,
но так как f(x)
вне интервала
равна
0 достаточно, чтобы она удовлетворяла:
Найдем
сначала неопределенный интеграл: Затем вычислим несобственный интеграл: Подставив
(**) в (*), окончательно получим
. Случайная
величина X задана плотностью
распределения ƒ(x) = 2x
в интервале (0,1); вне этого интервала
ƒ(x) = 0. Найти математическое
ожидание величины X. Р Подставив
a = 0, b = 1,
ƒ(x) = 2x,
получим Ответ:
2/3. Случайная
величина X задана плотностью
распределения ƒ(x) = (1/2)x
в интервале (0;2); вне этого интервала
ƒ(x) = 0. Найти математическое
ожидание величины X. Р Подставив
a = 0, b = 2,
ƒ(x) = (1/2)x,
получим М
(Х) =
Ответ:
4/3. Случайная
величина X в интервале (–с, с) задана плотностью распределения ƒ Р Подставив
a = –с, b = c,
ƒ(x) = , получим Учитывая,
что подынтегральная функция нечетная
и пределы интегрирования симметричны
относительно начала координат, заключаем,
что интеграл равен нулю. Следовательно,
М(Х) = 0. Этот
результат можно получить сразу, если
принять во внимание, что кривая
распределения симметрична относительно
прямой х = 0. Случайная
величина Х в интервале (2, 4) задана
плотностью распределения f(x)= Случайная
величина Х в интервале (3, 5) задана
плотностью распределения f(x)= Решение.
Представим плотность распределения в
виде
Случайная
величина Х в интервале (-1, 1) задана
плотностью распределения
В теории вероятностей приходится иметь дело со случайными величинами, все значения которых нельзя перебрать. Например, нельзя взять и «перебрать» все значения случайной величины $X$ - время службы часов, поскольку время может измеряться в часах, минутах, секундах, миллисекундах, и т.д. Можно лишь указать некоторый интервал, в пределах которого находятся значения случайной величины. Непрерывная случайная величина
- это случайная величина, значения которой целиком заполняют некоторый интервал. Поскольку перебрать все значения непрерывной случайной величины не представляется возможным, то задать ее можно с помощью функции распределения. Функцией распределения
случайной величины $X$ называется функция $F\left(x\right)$, которая определяет вероятность того, что случайная величина $X$ примет значение, меньшее некоторого фиксированного значения $x$, то есть $F\left(x\right)=P\left(X < x\right)$. Свойства функции распределения: 1
. $0\le F\left(x\right)\le 1$. 2
. Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$, равна разности значений функции распределения на концах этого интервала: $P\left(\alpha < X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$. 3
. $F\left(x\right)$ - неубывающая. 4
. ${\mathop{lim}_{x\to -\infty } F\left(x\right)=0\ },\ {\mathop{lim}_{x\to +\infty } F\left(x\right)=1\ }$. Пример 1
$$P\left(0,3 < X < 0,7\right)=F\left(0,7\right)-F\left(0,3\right)=0,7-0,3=0,4.$$ Функция $f\left(x\right)={F}"(x)$ называется плотностью распределения вероятностей, то есть это производная первого порядка, взятая от самой функции распределения $F\left(x\right)$. Свойства функции $f\left(x\right)$. 1
. $f\left(x\right)\ge 0$. 2
. $\int^x_{-\infty }{f\left(t\right)dt}=F\left(x\right)$. 3
. Вероятность того, что случайная величина $X$ примет значения из интервала $\left(\alpha ;\ \beta \right)$ - это $P\left(\alpha < X < \beta \right)=\int^{\beta }_{\alpha }{f\left(x\right)dx}$. Геометрически это означает, что вероятность попадания случайной величины $X$ в интервал $\left(\alpha ;\ \beta \right)$ равна площади криволинейной трапеции, которая будет ограничена графиком функции $f\left(x\right)$, прямыми $x=\alpha ,\ x=\beta $ и осью $Ox$. 4
. $\int^{+\infty }_{-\infty }{f\left(x\right)}=1$. Пример 2
. Непрерывная случайная величина $X$ задана следующей функцией распределения $F(x)=\left\{\begin{matrix} Математическое ожидание непрерывной случайной величины $X$ вычисляется по формуле $$M\left(X\right)=\int^{+\infty }_{-\infty }{xf\left(x\right)dx}.$$ Пример 3
. Найдем $M\left(X\right)$ для случайной величины $X$ из примера $2$. $$M\left(X\right)=\int^{+\infty }_{-\infty }{xf\left(x\right)\ dx}=\int^1_0{x\ dx}={{x^2}\over {2}}\bigg|_0^1={{1}\over {2}}.$$ Дисперсия непрерывной случайной величины $X$ вычисляется по формуле $$D\left(X\right)=\int^{+\infty }_{-\infty }{x^2f\left(x\right)\ dx}-{\left}^2.$$ Пример 4
. Найдем $D\left(X\right)$для случайной величины $X$ из примера $2$. $$D\left(X\right)=\int^{+\infty }_{-\infty }{x^2f\left(x\right)\ dx}-{\left}^2=\int^1_0{x^2\ dx}-{\left({{1}\over {2}}\right)}^2={{x^3}\over {3}}\bigg|_0^1-{{1}\over {4}}={{1}\over {3}}-{{1}\over {4}}={{1}\over{12}}.$$ Математическим ожиданием
дискретной случайной величины называется: В случае бесконечного множества значений в правой части (4.4) находится ряд, и мы будем рассматривать только те значения Х, для которых этот ряд абсолютно сходится. М(Х)
представляет собой среднее ожидаемое значение случайной величины. Оно обладает следующими свойствами: 1) М(С)=С, где С=const
2) M (CX)=CM (X) (4.5)
3) M (X+Y)=M(X)+M(Y), для любых Х и Y.
4) M (XY)=M (X)M(Y), если Х и Y независимы.
Для оценки степени рассеяния значений случайной величины около ее среднего значения M(X)=а
вводятся понятия дисперсии
D(X)
и среднего квадратического (стандартного) отклонения . Дисперсией
называется математическое ожидание квадрата разности (X- ),
т.е. : D(X)=M(X- ) 2 = p i ,
Где =М(X);
определяется как квадратный корень из дисперсии, т.е. Для вычисления дисперсии пользуются формулой: Свойства дисперсии и среднего квадратического отклонения: 1) D(C)=0, где С=сonst
2) D(CX)=C 2 D(X), (CX)= çCç (X) (4.7)
3) D(X+Y) =D(X)+D(Y),
если Х и У независимы. Размерность величин и совпадает с размерностью самой случайной величины Х, а размерность D(X) равна квадрату размерности случайной величины Х. 4.3. Математические операции над случайными величинами.
Пусть случайная величина Х принимает значения с вероятностями а случайная величина Y- значения с вероятностями Произведение КX случайной величины Х на постоянную величину К - это новая случайная величина, которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные произведениям на К значений случайной величины Х. Следовательно, ее закон распределения имеет вид таблица 4.2: Таблица 4.2 Квадрат
случайной величины Х, т.е. , - это новая случайная величина,которая с теми же вероятностями, что и случайная величина Х, принимает значения, равные квадратам ее значений. Сумма
случайных величин Х и У - это новая случайная величина, которая принимает все значения вида с вероятностями , выражающими вероятность того, что случайная величина Х примет значение а У - значение , то есть
(4.8)
Если случайные величины Х и У независимы, то: Аналогично определяются разность и произведение случайных величин Х и У. Разность
случайных величин Х и У - это новая случайная величина, которая принимает все значения вида , а произведение
- все значения вида с вероятностями, определяемыми по формуле (4.8), а если случайные величины Х и У независимы, то по формуле (4.9). 4.4. Распределения Бернулли и Пуассона
.
Рассмотрим последовательность n идентичных повторных испытаний, удовлетворяющих следующим условиям: 1. Каждое испытание имеет два исхода, называемые успех и неуспех. Эти два исхода - взаимно несовместные и противоположные события. 2. Вероятность успеха, обозначаемая p, остается постоянной от испытания к испытанию. Вероятность неуспеха обозначается q. 3. Все n испытаний - независимы. Это значит, что вероятность наступления события в любом из n повторных испытаний не зависит от результатов других испытаний. Вероятность того, что в n независимых повторных испытаниях, в каждом из которых вероятность появления события равна , событие наступит ровно m раз (в любой последовательности), равна Выражение (4.10) называется формулой Бернулли. Вероятности того, что событие наступит: а) менее m раз, б) более m раз, в) не менее m раз, г) не более m раз - находятся соответственно по формулам: Биномиальным называют закон распределения дискретной случайной величины Х - числа появлений события в n независимых испытаниях, в каждом из которых вероятность наступления события равна р; вероятности возможных значений Х = 0,1,2,..., m,...,n
вычисляются по формуле Бернулли (таблица 4.3).
Таблица 4.3 Так как правая часть формулы (4.10) представляет общий член биноминального разложения , то этот закон распределения называют биномиальным
. Для случайной величины Х, распределенной по биноминальному закону, имеем. Определение 13.1.
Случайная величина Х называется дискретной
, если она принимает конечное либо счётное число значений. Определение 13.2.
Законом распределения случайной величины Х
называется совокупность пар чисел ( , ), где – возможные значения случайной величины, а – вероятности, с которыми случайная величина принимает эти значения, т.е. = P{X
= }, причём =1. Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины и соответствующие им вероятности. Такая таблица называется рядом распределения
дискретной случайной величины. Ряд распределения можно изобразить графически. В этом случае по оси абсцисс откладывается , по оси ординат – вероятность . Точки с координатами ( , ) соединяют отрезками и получают ломаную, называемую многоугольником распределения,
который является одной из форм задания закона распределения дискретной случайной величины. Пример 13.3.
Построить многоугольник распределения случайной величины Х с рядом распределения Определение 13.4.
Говорят, что дискретная случайная величина Х имеет биноминальное распределение
с параметрами (n,p
)если она может принимать целые неотрицательные значения k
{1,2,…,n
} с вероятностями Р(Х=х
)=
. Ряд распределения имеет вид: Сумма вероятностей =
=1. Определение 13.5.
Говорят, что дискретная форма случайной величины Х
имеет распределение Пуассона
с параметром ( >0),если она принимает целые значения k
{0,1,2,…} с вероятностями Р(Х=k
)= . Ряд распределения имеет вид Так как разложение в ряд Маклорена имеет следующий вид , тогда сумма вероятностей = = =1. Обозначим через Х
число испытаний, которые нужно провести до первого появления события А
в независимых испытаниях, если вероятность появления А в каждом из них равна p
(0< p
<1), а вероятность непоявления . Возможными значениями Х
являются натуральные числа. Определение 13.6.
Говорят, что случайная величина Х
имеет геометрическое распределение
с параметром p
(0< p
<1), если она принимает натуральные значения k
N с вероятностями Р(Х=k)= , где .
Ряд распределения: Сумма вероятностей = = =1. Пример 13.7.
Монета брошена 2 раза. Составить ряд распределения случайной величины Х числа выпадений «герба». P 2 (0)= = ; P 2 (1)= = =0,5; P 2 (2)= = . Ряд распределения примет вид: Пример 13.8.
Из орудия стреляют до первого попадания по цели. Вероятность попадания при одном выстреле 0,6. произойдёт попадание при 3-м выстреле. Поскольку p
=0,6, q
=0,4, k
=3, тогда Р(А
)= =0,4 2 *0,6=0,096. Полностью характеризует случайную величину закон распределения, однако часто он бывает неизвестен, поэтому приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами (параметрами), описывающими случайную величину суммарно. Они называются числовыми характеристиками
случайной величины. К ним относятся: математическое ожидание, дисперсия и др. Определение 14.1.
Математическим ожиданием
дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности. Обозначают математическое ожидание случайной величины Х
через МХ
=М(Х
)=ЕХ
. Если случайная величина Х
принимает конечное число значений, то МХ
= . Если случайная величина Х
принимает счетное число значений, то МХ
= , причём математическое ожидание существует, если ряд сходится абсолютно. Замечание 14.2.
Математическое ожидание некоторое число, приближённо равное определённому значению случайной величины. Пример 14.3.
Найти математическое ожидание случайной величины Х
, зная её ряд распределения МХ
=3*0,1+5*0,6+2*0,3=3,9. Пример 14.4.
Найти математическое ожидание числа появлений события А
в одном испытании, если вероятность события А
равна p
. Случайная величина Х
– число появления события A
в одном испытании. Она может принимать значения =1 (A
наступило) с вероятностью p
и =0 с вероятностью , т.е. ряд распределения Отсюда МС=С*1=С. Замечание 14.6.
Произведение постоянной величины С на дискретную случайную величину Х
Определяется как дискретная случайная величина СХ
, возможные значения которой равны произведениям постоянной С на возможные значения Х
, вероятности этих значений СХ
равны вероятностям соответствующих возможных значений Х
. Свойство 14.7.
Постоянный множитель можно выносить за знак математического ожидания: М(СХ
)=С∙МХ
. Если случайная величина Х
имеет ряд распределения Ряд распределения случайной величины М(СХ
)= = = С∙М(Х
). Определение 14.8.
Случайные величины , ,…, называются независимыми
, если для , i
=1,2,…,n
Р{ , ,…, }= Р{ } Р{ }… Р{ } (1) Если в качестве = , i
=1,2,…,n
, то получим из (1) Р{ < , < ,…, < }= Р{ < }Р{ < }… Р{ < }, откуда получается другая формула: ( , ,…, ) = () ()... () (2) для совместной функции распределения случайных величин , ,…, , которую можно также взять в качестве определения независимости случайной величины. Свойство 14.9.
Математическое ожидание произведения 2-х независимых
случайных величин равно произведению их математических ожиданий: М(ХУ
)=МХ
∙МУ
. Свойство 14.10.
Математическое ожидание суммы 2-х случайных величин равно сумме их математических ожиданий: М(Х+У
)=МХ
+МУ
. Замечание 14.11.
Свойства 14.9 и 14.10 можно обобщать на случай нескольких случайных величин. Пример 14.12.
Найти математическое ожидание суммы числа очков, которые могут выпасть при бросании 2-х игровых костей. Пусть Х
число очков, выпавших на первой кости, У
число очков, выпавших на второй кости. Они имеют одинаковые ряды распределения: Тогда МХ
=МУ
= (1+2+3+4+5+6)= = . М(Х+У
)=2* =7. Теорема 14.13.
Математическое ожидание числа появлений события А
в n
независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: МХ
=np
. Пусть Х
– число появлений события А
в n
независимых испытаниях. –число появлений события А
в i
-том испытании, i
=1,2,…,n.
Тогда = + +…+ . По свойствам математического ожидания МХ
= . Из примера 14.4 MX i
=p, i
=1,2,…,n,
отсюда МХ
= =np
. Определение 14.14.
Дисперсией
случайной величины называется число DX
=M(X
-MX
) 2 . Определение 14.15.
Средним квадратическим отклонением
случайной величины Х
называется число =. Замечание 14.16.
Дисперсия является мерой разброса значений случайной величины вокруг её математического ожидания. Она всегда неотрицательна. Для подсчёта дисперсии удобнее пользоваться другой формулой: DX
= M(X
- MX
) 2 = M(X
2 - 2X∙
MX
+ (MX
) 2) = M(X
2) - 2M(X∙
MX
) + M(MX
) 2 = =M(X
2)-MX∙
MX+
(MX
) 2 =
M(X
2) - (MX
) 2 . Отсюда DX
= M(X
2) - (MX
) 2 . Пример 14.17.
Найти дисперсию случайной величины Х
, Заданной рядом распределения MX
=2*0,1+3*0,6+5*0,3=3,5; M(X
2)= 4*0,1+9*0,6+25*0,3=13,3; DX
=13.3-(3,5) 2 =1,05. Свойства дисперсии
Свойство 14.18.
Дисперсия постоянной величины равна 0: DC = M(С- MС) 2 = M(С- С) 2 =0. Свойство 14.19.
Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат D(СX
) =C 2 DX
. D(CХ)=М(С- CMX
) 2 =М(С(X- MX
) 2) = C 2 M(X
- MX
) 2 = C 2 DX
. Свойство 14.20.
Дисперсия суммы 2-х независимых
случайных величин равна сумме дисперсий этих величин D(Х+Y
)=DХ
+DY
. D(X + У
)=М((X + Y
) 2) – (M(X + Y
)) 2 = M(X 2 +
2XY + Y 2
) - (MX
+ MY
) 2 = =M(X
) 2 +2МХ
МY
+M(Y
2)-(M(X
) 2 +2МХ
МY
+M(Y
) 2)= M(X
2)-(MX
) 2 +M(Y
2)- (MY
) 2 = = DX
+DY
. Следствие 14.21.
Дисперсия суммы нескольких независимых
случайных величин равна сумме их дисперсий. Теорема 14.22.
Дисперсия числа появлений события А
в n
независимых испытаниях, в каждом из которых вероятность p) 2 =). Отсюда D +2 ,
Отсюда
,
или.
.
Отсюда
,
или.
При
x=0 производная
не
существует.
в
интервале
;
вне этого интервала
.
Найти вероятность того, что X
примет значение, принадлежащее интервалу
.
.
Следовательно, искомая вероятность
.
. (*)
.
.
. (*)
.
.
. (*)
(**)
Потребуем,
чтобы это условие выполнялось для
заданной функции:
.
. (*)
(**)
ешение.
Используем формулу
ешение.
Используем формулу
=
4/3
(x)
= ; вне этого интервала ƒ(x)
= 0. Найти математическое ожидание
величины X.
ешение.
Используем формулу
.
Отсюда видно, что при х=3 плотность
распределения достигает максимума;
следовательно,
.
Кривая распределения симметрична
относительно прямой х=3, поэтому
и
.
;
вне этого интервала f(x)=0. Найти моду,
математическое ожидание и медиану
величины Х.
.
Отсюда видно, что при х=3 плотность
распределения достигает максимума;
следовательно,
.
Кривая распределения симметрична
относительно прямой х=4, поэтому
и
.
;
вне этого интервала f(x)=0. Найти: а) моду;
б) медиану Х.
Функция распределения непрерывной случайной величины
0,\ x\le 0\\
x,\ 0 < x\le 1\\
1,\ x>1
\end{matrix}\right.$. Вероятность попадания случайной величины $X$ в интервал $\left(0,3;0,7\right)$ можем найти как разность значений функции распределения $F\left(x\right)$ на концах этого интервала, то есть:Плотность распределения вероятностей
0,\ x\le 0\\
x,\ 0 < x\le 1\\
1,\ x>1
\end{matrix}\right.$. Тогда функция плотности $f\left(x\right)={F}"(x)=\left\{\begin{matrix}
0,\ x\le 0 \\
1,\ 0 < x\le 1\\
0,\ x>1
\end{matrix}\right.$Математическое ожидание непрерывной случайной величины
Дисперсия непрерывной случайной величины
.
(4.6)
...
...
(4.10)
Число успехов Х=m
...
m
...
n
Вероятность Р
...
...
Х
…
…
Р
…
…
Х
Р
0,1
0,3
0,2
0,4
Х
…
k
…
n
Р
…
…
Х
…
k
…
Р
…
…
Х
…
n
…
Р
…
…
Х
Р
14 Числовые характеристики дискретных случайных величин
Х
Р
0,1
0,6
0,3
Х
…
…
Р
…
…
СХ
…
…
Р
…
…
Х
Р
X
P
0,1
0,6
0,3